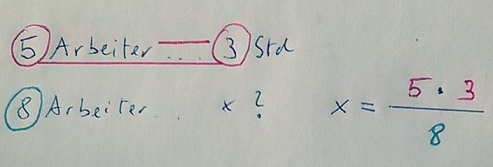Arbeitsplaner 2b

Do, 28.5. 2020

Heute gibt es ein paar gemischte Aufgaben zur Prozentrechnung:

1. Rechne im Kopf. Wie viel sind:
a) 10 % von 37,50 €?       b) 1 % von 1807 kg?       c) 25 % von 84 m ? d) 50 % von 52 €

2. Wie viel sind:
a) 24 % von 70 €?       b) 73 % von 55 €?

3. Ein Kleid kostet 80 €. Im Sommerschlussverkauf gibt es -70%. Wie viel kostet das Kleid jetzt?

4. Herr Maier fährt auf Urlaub. Er fährt 25 % der Strecke, dann muss er tanken.
Wie weit fährt er insgesamt, wenn die Tankstelle 112 km von seiner Wohnung entfernt ist?

5. Tobias hat bei der Schulsprecherwahl 78 von 202 Stimmen bekommen. Wie viel Prozent sind das?
(Runde auf eine Stelle nach dem Komma!)

Mo, 25.5. 2020

Ich habe hier das Wichtigste von letzter Woche zur Prozentrechnung zusammengeschrieben.

Wer heute zu Hause ist, macht folgende Aufgaben:

1076, 1077 ... Hier musst du nichts rechnen! Schreib nur: was ist hier der Grundwert, der Prozentsatz und der Prozentanteil.
1107, 1108 ... Hier musst du den Prozentsatz berechnen.
1118 ... Hier musst du den Grundwert berechnen, also: Wie viel sind 100 %?

Do, 14.5. 2020

Wichtige Prozentsätze

Genau wie bei den Brüchen sollte man sich auch diese Prozentsätze merken:

50 % = 0,5 = 1/2 (Die Hälfte)
25 % = 0,25 = 1/4
75 % = 0,75 = 3/4
33,3... % = 0,333... = 1/3
10 % = 0,1 = 1/10

Beispiele:
50 % von 28 ... Ich rechne die Hälfte von 28:     28 : 2 = 14.
25 % von 12 ... Ich rechne ein Viertel von 12:     12 : 4 = 3
75 % von 36 ... Ich rechne drei Viertel von 36:     36 : 4 = 9; 9 · 3 = 27
33,3 % von 12 ... Ich rechne ein Drittelvon 12:     12 : 3 = 4
10 % von 74 ... Ich rechne ein Zehntel von 74 (Komma verschieben!!!):  74 : 10 = 7,4

Aufgabe 1: Rechne im Kopf!
a) 50 % von 44         b) 10 % von 11         c) 25 % von 32         d) 75 % von 32
e) 10 % von 12,8       f) 33,3 % von 63       g) 50 % von 15         h) 25 % von 80


Du hast gestern gesehen: 60 % von 50 ist dasselbe wie 50 % von 60.
Man kann also die Zahlen vertauschen.

Aufgabe 2: Rechne vorteilhaft!

a) 14 % von 50         b) 38 % von 10         c) 12 % von 25         d) 8 % von 75



Aufgabe 3: Hier musst du so wie gestern rechnen.
a) 2 % von 129         b) 11 % von 84         c) 23 % von 5000         d) 6 % von 14,3

Mi, 13.5. 2020

|     Wir haben gestern gesehen:
|     1 % = 1 / 100

Wie viel ist 1 % von 244 €? Wir müssen einfach 244 durch 100 dividieren!

244 : 100 = 2,44

1 % von 244 € sind 2,44 €

Ergänze den folgenden Satz:

Bei der Division durch 100 wird das Komma ..................... verschoben.

Aufgabe 1: Wie viel ist 1 % von ...
a) 183         b) 2000       c) 17       d) 5
e) 624 €       f) 43 m       g) 1 kg     h) 100 Personen


|     Wenn 1 % von 244 € = 2,44 € ist, dann sind natürlich 3 % von 244 = 3 · 2,44 = 7,32 €.


Aufgabe 2: Wie viel sind ...
a) 3 % von 183         b) 7% von 2000       c) 10 % von 17       d) 12 % von 5
e) 5 % von 624 €       f) 20 % von 43 m       g) 8 % von 1 kg     h) 41 % von 100 Personen



Aufgabe 3: Wie viel sind ...
a) 50 % von 12         b) 10% von 61,4       c) 25 % von 40       d) 100 % von 888,999
e) 75 % von 4           f) 200 % von 13       g) 60 % von 50     h) 50 % von 60

Di, 12.5. 2020

Heute kommen wir langsam zur Prozentrechnung.

1. Schreibe als Dezimalzahl:

a) 13/100 =         b) 7/100 =         c) 95/100 =         d) 200/100 =


2. Erweitere auf Hunderstel:

Bsp.: 7 / 20 = 7 · 5 / 20 · 5 = 35/100

a) 1/5 = ... / 100         b) 13/50 =         c) 3/4 =         d) 6/25 =


3. Schreibe als Hundertstel:

Bsp.: 0,02 = 2/100;     0,4 = 40/100

a) 0,26 = ... / 100         b) 0,5 =         c) 1,2 =         d) 0,09 =


Statt Hunderstel kann man auch Prozent schreiben:

1 Prozent = 1 Hundertstel
1 % = 1 / 100

Also:
0,31 = 31/100 = 31 %
0,05 = 5/100 = 5 %
Die Hälfte = 1/2 = 50/100 = 50%
3/4 = 0,75 = 75/100 = 75 %

4. Schreibe als Prozent:

a) 0,01 = ... %         b) 33/100 = ... %         c) 0,04 = ... %         d) 0,4 = ... %
e) 1 = ... %         f) 2/5 = ... / 100 = ... %         g) 1,5 = ... %         h) 1/4 = ... %

Mo, 11.5. 2020

Heute gibt es ein paar Aufgaben zur Wiederholung:

1. Schreibe als Dezimalzahl:

a) 1/4 =         b) 1/2 =         c) 3/4 =         d) 1/10 =
e) 1/8 =         f) 1/3 =         g) 1/100 =         h) 1/1000 =

2. a) Nenne alle Teiler von 27.
    b) Nenne die ersten 5 Vielfachen von 13.

3. Ein Rechteck hat die Seiten a = 4,2 cm; b = 9 cm. Berechne Umfang und Flächeninhalt!

4. a) 17 cm = ... m;       b) 1 m 4 cm = ... m = ... cm;       c) 3 m 5 cm + 402 mm = ... m

    d) 16 cm² = ... mm²;       e) 8,4 m² = ... cm²;       f) 71 m² = ... a

5. a) 7 Schafe kommen mit dem Futter 18 Tage aus. Wie lange würden 5 Schafe mit derselben Futtermenge auskommen?

  b) Sonja braucht mit dem Rad für 700 m 4 Minuten. Wie weit kommt sie in 10 Minuten??

Do, 7.5. 2020

Die heutigen Aufgaben sind:

BS 160 / 872, 874
BS 161 / 881 a), 882 a), 883
++ 884

Schreib mir die Gleichung, die du erstellt hast, und die Lösung.

Statt einer Textaufgabe, die du nicht verstehst, kannst du dir auch zwei Gleichungen von BS 159 / 870 aussuchen und lösen.
(Wenn du keine Textaufgabe machst, solltest du also mindestens 10 von den einfachen Gleichungen lösen, oder 12 für ein Extra-Plus.)

Hier gibt es auch wieder die Angaben zum Nachlesen. (Außer 870)

Mi, 6.5. 2020

Bei Textgleichungen ist es besonders wichtig, die Angaben genau zu lesen und die Probe zu machen.

Bei Aufgabe 878 stehen zum Beispiel zwei Informationen in der Angabe:
1. Hannes bekommt um 5 € mehr als Michi.
2. Zusammen bekommen beide 20 €.

Die Lösung kann nicht 5 € und 15 € sein. 15 € ist um 10 € mehr als 5 €, nicht um 5 € mehr.
Die Lösung kann nicht 10 € und 15 € sein. 15 € ist um 5 € mehr als 10 €, aber zusammen macht es 25 €.

Mit einer Gleichung ist es ganz einfach:

Michi ... x €
Hannes ... x + 5 €
Zusammen ... x + x + 5 = 20

2 x + 5 = 20 | -5
2 x = 15 | : 2
x = 7,5

A: Michi bekommt 7,50 €.
Hannes bekommt 12,50 €.

Wir kontrollieren noch, ob die Lösung zu der Angabe passt:
1. 12,50 € ist um 5 € mehr als 7,50 € ✔
2. 7,50 € + 12,50 € = 20 € ✔

Versuche jetzt, die folgenden Gleichungen genau so zu lösen:

Ü 6.5.1
a) Didi und Kiki haben zusammen 17 Bücher. Kiki hat um 3 Bücher mehr als Didi. Wie viele Bücher hat jeder?

b) Lara hat um 125 € mehr als Clara. Zusammen haben sie 200 €. Wie viel Geld hat jede?

c) Benno hat um 5 Buntstifte weniger als Menno. Gemeinsam haben sie 23 Buntstifte. Wie viele Buntstifte hat jeder?

d) Resi und Mesi haben zusammen 43,40 €. Mesi hat um 16,70 € mehr als Resi. Wie viel hat jede?


Hier musst du schon anders rechnen:

e) Max hat doppelt so viel Geld wie Moritz. Zusammen haben sie 120 €. Wie viel Geld hat Max?

++ f) Bill hat 3 mal so viel Geld wie Steve. Steve hat um 4 Mrd. € weniger als Bill. Wie viel Geld hat jeder?

Di, 5.5. 2020

Heute schauen wir uns Textgleichungen an.

Bei BS 160 / 871 musst du zuerst zu jedem Text die passende Gleichung aus den unteren Kästchen finden. Dann erst gib die Lösung an!

Bei BS 161 / 878 und 879 musst du zuerst eine passende Frage finden. Dann schreib dazu eine Gleichung und löse sie.

Beispiel: Bei BS 161 / 880 würdest du so vorgehen:

Mutter und Vater sind zusammen 81 Jahre alt. Der Vater ist um 9 Jahre älter als die Mutter.

Die Frage könnte z.B. lauten:
Wie alt ist die Mutter?

Für das Alter der Mutter brauche ich eine Variable. Ich kann sie z.B. x oder m (für Mutter) nennen.

Dann überlege ich:
Alter der Mutter ... m Jahre
Alter des Vaters ... m + 9 Jahre (weil der Vater um 9 Jahre älter ist.)

Zusammen: m + m + 9 = 81

Jetzt kann ich die Gleichung lösen:
m + m + 9 = 81
2m + 9 = 81 | -9
2m = 72 | : 2
m = 36

A: Die Mutter ist 36 Jahre alt.

Pr.: 36 + 36 + 9 = 81 ✔

Mo, 4.5. 2020

Heute kommt noch ein Schritt dazu. Schau dir diese Gleichung an:

5x - 1 = 3x + 9

Hier nehme ich als erstes auf beiden Seiten 3x weg:

5x - 1 = 3x + 9 | -3x
2x - 1 = 9

Jetzt kann ich die Gleichung so wie am Donnerstag lösen:

2x - 1 = 9 | +1
2x = 10 | : 2
x = 5

Für die Probe schreibe ich in der ersten Gleichung 5 statt x.
Ich rechne nach, ob links und rechts das selbe herauskommt:

Links: 5 · 5 - 1 = 25 - 1 = 24
Rechts: 3 · 5 + 9 = 15 + 9 = 24 ✔

Löse nun folgende Gleichungen:

Ü 4.5.1
a) 7x - 2 = 4x + 10       (Wenn du dir nicht sicher bist, kannst du hier die Lösung vergleichen.)
b) 9x + 3 = 8x + 15
c) 11x + 4,5 = 7x + 20,5
d) 100x - 18 = 90x + 33


Ü 4.5.2 Diese Gleichungen sind wieder einfacher:
a) 3t + 4 = 28
b) 6z - 5 = 4
c) 12 k - 12 = 24

Do, 30. 4. 2020

Zum Aufwärmen fangen wir mit den Übungen BS 158 / 850 und 851 an.
Achte auf die unterschiedlichen Rechenarten!

Dann schauen wir uns die komplizierteren Gleichungen BS 159 / 867, 868 und 869 an.

Hier musst du in 2 Schritten rechnen. Zum Beispiel:

5x - 9 = 11
(Hinweis: 5x bedeutet dasselbe wie 5 · x)

1.) Wir addieren 9. (Man schreibt: 5x - 9 = 11 | + 9)
5x = 11 + 9
5x = 20

2.) Wir dividieren durch 5. (Man schreibt: 5x = 20 | : 5)
x = 20 : 5
x = 4

Für die Probe rechnen wir nach: 5 · 4 - 9 = ???
Da sollte wieder 11 herauskommen.

Noch ein Beispiel. Diesmal schreibe ich die Erklärungen nicht mehr dazu.

3 + 4 x = 27
Wir schreiben:

3 + 4 x = 27 | - 3
4 x = 24 | : 4
x = 6

Pr: 3 + 4 · 6 = 3 + 24 = 27

Wenn du dir nicht sicher bist, kannst du hier die ersten Lösungungen von jeder Übung kontrollieren:
(Markiere den schwarzen Balken, um die Lösung zu sehen)

867 a) x = 5     868 a) x = 3     869 a) x = 3

Hier gibt es auch wieder die Angaben zum Nachlesen.

Mi, 29. 4. 2020

Nach den Verhältnissen schauen wir uns heute ein paar Gleichungen an.
Mach die Übungen BS 156 / 842, 843, 844, 845 und 846.

Statt x musst du eine Zahl finden, so dass die Rechnung stimmt.

z.B. 844 a) x + 5 = 14

Welche Zahl kann ich statt x schreiben, um eine richtige Rechnung zu bekommen?
Die Antwort ist natürlich 9, weil 9 + 5 = 14!

Ich schreibe als Lösung: x = 9

Probe bedeutet: Ich rechne nochmal nach, ob 9 + 5 = 14.
Das wird erst bei schwierigeren Gleichungen wichtig sein.

Hier gibt es auch wieder die Angaben zum Nachlesen.

Di, 28. 4. 2020

Die heutigen Aufgaben sind:
691 ... rechne b) 50 km/h statt 110 km/h!

693, 694: Die mittlere oder durchschnittliche Geschwindigkeit bedeutet:
Wie viele km fährt man in 1 Stunde (oder in 60 Minuten)?

695

Wenn du Hilfe brauchst habe ich hier ein paar Tipps.

Hier gibt es auch wieder die Angaben zum Nachlesen.

Mo, 27. 4. 2020

Die heutigen Aufgaben sind 679, 686, 688, 689 und 690. (Sie sind im Buch S. 119 bzw. S. 120.)
Auch hier musst du wieder überlegen, ob es sich um ein direktes oder indirektes Verhältnis handelt!

Hier gibt es auch wieder die Angaben zum Nachlesen.

Do, 23. 4. 2020

Wenn du alle Aufgaben zu direktem und indirektem Verhältnis richtig gerechnet hast, wirst du gemerkt haben, dass man alles nach dem selben Muster rechnen kann. Mann nennt so eine Rechnung

            Schlussrechnung

Am Besten geht man so vor:

Man schreibt die Angaben untereinander:

   5 Stk ... 3 €
   8 Stk ... x €

oder:

   5 Arbeiter ... 3 Std.
   8 Arbeiter ... x Std.

Dann muss man herausfinden, ob es ein direktes oder ein indirektes Verhältnis ist.

Beim direktem Verhältnis (doppelt so viel von einem bedeutet doppelt so viel vom anderen) rechnest du so:



Beim indirektem Verhältnis (doppelt so viel von einem bedeutet die Hälfte vom anderen) rechnest du so:




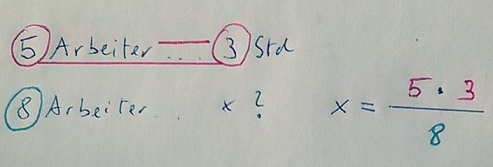
(Du kannst natürlich auch so wie bisher rechnen:
Wie viel kostet 1 Stück?
Wie viele Stunden würde1 Arbeiter alleine brauchen?)

- - - - - - - - - - -

Überlege dir bei jeder dieser Aufgaben, ob es sich um ein direktes oder indirektes Verhältnis handelt, und berechne dann das Ergebnis:

Ü 23.4: Direkt oder indirekt?

1.) 12 Saftflaschen wiegen 18 kg. Wie viel wiegen 7 Flaschen?

2.) Im Kino zahlen 9 Schüler 43,20 €. Wie viel müssen 15 Schüler zahlen?

3.) Die Erdbeeren auf dem Feld müssen geerntet werden. 3 Helfer brauchen dafür 16 Stunden. Wie lange müssten 5 Helfer arbeiten?

4.) Pauls alte Schule war 750 m von seiner Wohnung entfernt. Er brauchte zu Fuß 12 Minuten.
Seine neue Schule ist 1,2 km entfernt. Wie lange braucht er jetzt, wenn er gleich schnell geht?

5.) Tina fährt mit dem Fahrrad in die Schule. Wenn sie mit 10 km/h fährt, braucht sie 7,5 Minuten.
Heute hat sie verschlafen und fährt deshalb mit 15 km/h. Wie lange braucht sie heute?

Mi, 22. 4. 2020

Die heutigen Aufgaben sind BS 118 / 668, 671 und 673.

Es sind wieder Aufgaben zum indirekten Verhältnis, deswegen rechnest du alle auf die gleiche Art, zum Beispiel:

671 a)
7 Arbeiter ... 51 Stunden
3 Arbeiter ... x Stunden

Erst multiplizieren: 7 x 51 = ?
Dann das Ergebnis durch 3 dividieren.



Wenn du kein Buch hast, kannst du hier die Angaben nachlesen.

Di, 21. 4. 2020

Heute gibt es noch ein paar Übungen zum indirekten Verhältnis:

BS 113 / 653, 654
BS 118 / 667 a) und b), 670


Wenn du noch Schwierigkeiten hast, kannst du hier eine Anleitung für 653 und 654 nachlesen.

Wenn du kein Buch hast, kannst du hier die Angaben nachlesen.

Mo, 20. 4. 2020

Heute schauen wir uns das indirekte Verhältnis an.

Indirektes Verhältnis (oder indirekt proportional) bedeutet:
Wenn doppelt so viel von einer Sache habe, habe ich nur halb so viel von einer anderen.
Wenn ich drei mal so viel von einer Sache habe, habe ich nur ein Drittel von einer anderen...

z.B.: Wenn ich doppelt so schnell fahre, brauche ich nur halb so lang für die Fahrt.
Wenn sich drei Leute einen Kuchen teilen, bekommt jeder nur ein Drittel vom Kuchen.


Macht nun im Buch S. 113 die Übungen 649, 650, 651 und 652.

Hier geht's zu den Angaben.

Fr, 17. 4. 2020

Macht heute im Buch S. 109 die Aufgaben 630, 633, 634 und 635.
Bei 634 und 635 ist die Frage jeweils: Welches Angebot ist günstiger?


630: Zwei Päckchen Sammelbilder kosten 1 €. Wie viel bezahlt man für fünf Päckchen?

633: Ein Bauer hat im vergangenen Jahr von einem 1,5 ha großen Feld 21 t Weizen geerntet.
In diesem Jahr hat er Weizen auf einem 2,5 ha großem Feld angebaut.
Wie viel t Weizen wird er etwa ernten können, wenn die Pflanzen so gut wachsen wie im Vorjahr?

634: Welches Angebot ist günstiger?
a) 2 kg Kartoffeln ... 1,26 €
    5 kg Kartoffeln ... 2,90 €

b) 2-er Packung Seife ... 1,86 €
    5-er Packung Seife ... 5,64 €

635: Welches Angebot ist günstiger?
a) 10 dag Extrawurst ... 1,26 €
      1 Stange ( 1 kg) ... 11 € €

b) 3 Schachteln Kekse ... 4,20 €
    10 Schachteln Kekse ... 12 €

Do, 16. 4. 2020

Macht heute im Buch S. 108 die Aufgaben 625, 627, 628 und 629.
Dann versucht die Tabelle 625.

Falls du Hilfe brauchst, kannst du hier nachlesen:

Lösung für BS 108 / 625

Anleitung für BS 108 / 626         Lösung für BS 108 / 626

Mi, 15. 4. 2020

Guten Morgen!
Ich hoffe, ihr hattet schöne Osterferien. Für den Anfang gibt es wieder ein paar Übungen zum Umrechnen:

Ü 15.4.1 a) 7 cm = ... mm;  7 cm² = ... mm²       b) 3,8 m = ... cm;  3,8 m² = ... cm²       c) 8 m 4 cm 2 mm = ... cm;  8 m² 4 cm² 2 mm² = ... cm²

Ü 15.4.2 a) 13 ha = ... a = ... m²;       b) 7,41 m + 35 cm + 18 mm = ?      c) 6,2 cm² + 18 mm² + 0,004 m² = ?

Als Nächstes schauen wir uns das direkte Verhältnis an.

Direktes Verhältnis (oder direkt proportional) bedeutet:
Wenn ich doppelt so viel von einer Sache habe, habe ich auch doppelt so viel von einer anderen.
Wenn ich drei mal so viel von einer Sache habe, habe ich auch drei mal so viel von einer anderen...

z.B.: Wenn ich doppelt so viele Äpfel kaufe, muss ich doppelt so viel bezahlen.
Wenn ich drei mal so viele Äpfel kaufe, muss ich drei mal so viel bezahlen.


Macht nun im Buch S. 105 die Übungen 613, 616 a) und 617 a).

Liebe Leute!

Ich erinnere euch daran, dass bei Quadraten und Rechtecken:

der Umfang eine Länge ist und daher in mm, cm, m... angegeben wird;

die Fläche aber in mm², cm², m²... angegeben wird!

Achtet bitte bei euren Antworten auf die richtigen Einheiten!!!

Do, 2. 4. 2020

Heute gibt es 3 Konstruktionen. Die Aufgabe ist jeweils:

* Zeichne ein Koordinatensystem (Einheit = 1 cm), trage die 4 Punkte ein und verbinde sie.
* Ist es ein Rechteck oder ein Quadrat?
* Berechne den Umfang und den Flächeninhalt.

1.) A (1 | 1); B (5 | 1); C (5 | 4); D (1 | 4)

2.) A (0 | 0,5); B (3,2 | 0,5); C (3,2 | 3,7); D (0 | 3,7)

3.) A (3 | 0); B (7 | 3); C (4 | 7); D (0 | 4)

Wer sich Pluspunkte verdienen möchte, kann sich heute oder morgen auch
die Textaufgaben 540 und 541 anschauen. Das ist aber eine freiwillige Zusatzaufgabe.

Mi, 1. 4. 2020

Heute gibt es die folgenden Übungen:

BS 83 / 518, 519
BS 84 / 527, 528
BS 85 / 534

Wer kein Buch hat,kann die Aufgaben hier nachlesen:
Aufgaben für 1. 4.

Di, 31. 3. 2020

Hier hast du deine Antworten von gestern vergleichen:
Lösungen vom Montag, 30.3.

Heute gibt es noch ein paar Übungen dazu.

Vergiss nicht, dass bei Flächeneinheiten jeder Sprung über 2 Stellen geht!

Also:
1,3 cm = 13 mm, aber 1,3 cm² = 130 mm²
528 cm = 5,82 m, aber 528 cm² = 0,0582 m
2 cm 7 mm = 27 mm = 2,7 cm, aber 2 cm² 7 mm² = 207 mm² = 2,07 cm²

Ü 31.3.1 a) 6 cm = .... mm 6 cm² = .... mm²	b) 3 m = .... cm 3 m² = .... cm²	c) 75 cm = .... m 75 cm² = .... m²
Ü 31.3.2 a) 1,2 m = .... cm 1,2 m² = .... cm²	b) 5cm 3 mm = .... cm 5 cm² 3 mm² = .... cm²	c) 4 m 4 cm = .... cm 4 m² 4 cm² = .... cm²
++Ü 31.3.3 a) 1 m = .... mm 1 m² = .... mm²	b) 2033 mm = .... m 2033 mm² = .... m²	c) 1 m 5 cm 3 mm = .... cm 1 m² 5 cm² 3 mm² = .... cm²

Wer will, kann auch noch BS 83 / 523 versuchen.

Mo, 30. 3. 2020

Wichtig! Fang erst mit der Aufgabe an, wenn du die Aufgaben von letzter Woche fertig hast!
Am Freitag hast du gesehen:

1cm² ist die Fläche von einem Quadrat mit der Seitenlänge 1 cm.
1dm² ist die Fläche von einem Quadrat mit der Seitenlänge 1 dm.

1 cm² = 100 mm²
1 dm² = 100 cm²

Genauso gilt: 1m² ist die Fläche von einem Quadrat mit der Seitenlänge 1 m.
1km² ist die Fläche von einem Quadrat mit der Seitenlänge 1 km.

1 m² = 10 000 cm²
1 km² = 1 000 000 m²

Zwischen einem Quadratmeter und einem Quadratkilometer gibt es noch zwei Einheiten:

Ein Ar (1 a) ist die Flächen von einem Quadrat mit der Seitenlänge 10 m. 1 a = 100 m²
Ein Hektar (1 ha) ist die Flächen von einem Quadrat mit der Seitenlänge 100 m. 1 ha = 10 000 m²

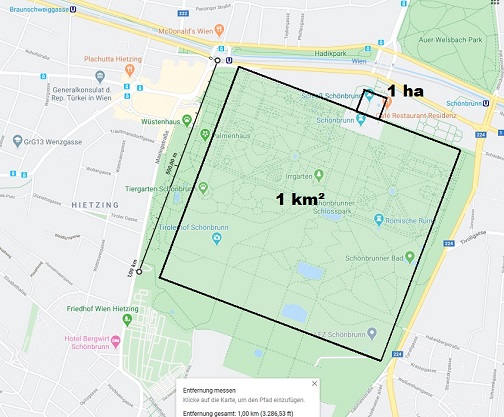
Auf diesem Bild siehst du:

Der Schönbrunner Schlosspark hat mehr als 1 km² Fläche.
Der Platz vor dem Schloss Schönbrunn ist etwas mehr als 1 ha.




Versuche nun die Aufgaben:

515 – Welche Einheit passt zu welchem Bild?
(Das musst du mir nicht schicken; ich werde die Lösung morgen hier posten.)

516 – Die Tabelle im Buch ausfüllen; Schreib mir dann nur die Lösungen aus der letzten (rechten) Spalte.

517 – Vergiss nicht, dass 1 cm² = 100 mm²!

Wer kein Buch hat, kann hier die Aufgaben nachlesen.

Fr, 27. 3. 2020

Versucht noch, bis spätestens Montag alle Aufgaben von dieser Woche fertig zu haben.

Als Vorübung für die Umrechnung von Flächen gibt es noch eine kleine Aufgabe:

1.) Konstruiere ein Quadrat mit der Seitenlänge 10 cm. Berechne die Fläche.
Konstruiere ein Quadrat mit der Seitenlänge 1 dm. Berechne die Fläche.
Was fällt dir auf?

2.) Konstruiere ein Quadrat mit der Seitenlänge 1 cm. Berechne die Fläche.
Konstruiere ein Quadrat mit der Seitenlänge 10 mm. Berechne die Fläche.
Was fällt dir auf?

Do, 26. 3. 2020

Fang erst mit den heutigen Aufgaben an, wenn du die Aufgaben von Mo, Di und Mi richtig gelöst hast!

1.) BS. 82 / 512
a) Ein Band ist 5 m lang und wird in 4 gleiche Teile geschnitten. Wie lang ist ein Teil?
b) Von einem 5 m langen Band wird ein 1,4 m langes Stück abgeschnitten. Der Rest wird in 12 gleiche Teile geteilt. Wie lang ist ein Teilstück?

2.) BS. 82 / 513 Die Länge eines Rohres beträgt 350 cm. Es soll eine 42 m lange Rohrleitung gelegt werden. Wie viele Rohre sind dafür erforderlich?

3.) Konstuiere ein Rechteck mit den Seiten a = 53 mm und b = 4 cm.
Berechne den Umfang und die Fläche.

Mi, 25. 3. 2020

Heute gibt es ein paar knifflige Übungen zum Umrechnen von Längen.

Beispiel:

2 cm 7 mm = 2,7 cm = 27 mm
5 dm 3 mm =5,03 dm = 50,3 cm = 503 mm
18 km 23 m = 18,023 km = 18 023 m
6 km 70 m = 6,07 km = 6 070 m

a) 1 m 1 dm = ......... m = ......... dm = ........ cm = ........ mm

b) 3 m 5 cm = ........ m = ........ cm

c) 7 m 8 mm = ........ m = ........ cm = ........ mm

d) 3 km 712 m = ........km = ........m

e) 1 km 20 m = ........ km = ........ m

f) 12 km 3 m = ........ km = ........ m

2. Hier kannst du selber wählen, in welcher Einheit du rechnen willst!

Beispiel:

53 mm + 2,4 cm = 5,3 cm + 2,4 cm = 7,7 cm
    oder
53 mm + 2,4 cm = 53 mm + 24 mm = 77 mm

23 cm + 23 mm = 23 cm + 2,3 cm = 25,3 cm
    oder
23 cm + 23 mm = 230 mm + 23 mm = 253 mm

a) 16 mm + 1,8 cm =

b) 2 m + 184 cm + 70 mm =

c) 0,06 m + 305 mm + 80 cm =

3. Und jetzt eine kleine Vorübung zu den Flächen. Zeichne ins Heft oder auf kariertem Papier.

a) Konstruiere ein Rechteck: a = 5 mm; b = 10 mm.

Wie viele Kästchen hat es?

b) Konstruiere noch ein Rechteck: a = 5 cm; b = 10 cm.

Wie viele Kästchen hat es? (Ausrechnen, nicht zählen!)

c) Ergänze:

Das Rechteck b) hat ........ mal so lange Seiten wie a).

Das Rechteck b) hat ........ mal so viele Kästchen wie a).

Fr, 20. 3. 2020

* Übungen zu Längenmaßen:

Für Mo 23.3.:

BS. 82 / 505 ... Ihr könnt die Tabelle im Buch ausfüllen und dann hier mit der Lösung vergleichen:

Hier geht's zur Aufgabe           Hier ist die Lösung

506 - Rechne in mm um: a) 5 cm; b) 145 cm; c) 3 cm 5 mm d) 1,75 dm

507 - Rechne in cm um: a) 7 dm; b) 8,2 dm; c) 4 cm 2 mm d) 350 mm

Für Di 24.3.:

508 - Rechne in dm um: a) 7 m; b) 8,3 m; c) 3 m 1 dm d) 165 cm

509 - Rechne in m um: a) 6 km; b) 2,8 km; c) 8 020 mm d) 675 cm

510 - Rechne in km um: a) 8 000 m; b) 3 078 m; c) 3 km 50 m d) 12 km 9 m

511 Rechne in gleiche Einheiten um und addiere:

a) 37 m 5 dm + 15 cm + 567 mm =

b) 4 km 12 m + 3 540 m + 5,8 km =

c) 324 mm + 5,6 cm + 8 dm 3 cm =

d) 0, 56 km + 7 km 70 m + 365 m =

Mi, 18. 3. 2020

* Für den Anfang gibt es ein paar Divisionen, die ich mit euch üben wollte:

1. Einfach:

a) 27 : 4 b) 193 : 5 c) 60,2 : 7

2. Zweistellig - Rechne, bis der Rest 0 ist!

a) 65,76 : 48 b) 27,54 : 34 c) 22 : 32

(Zusatzübung für besonders fleißige) d) 12,27 : 17 e) 5891 : 25 f) 189 : 14

3. Mit Periode

a) 527 : 18 b) 449 : 66 c) 98 : 88

Hier geht's zu den Lösungen

* Als Wiederholung für Rechteck und Quadrat kannst du dir außerdem im Buch S. 87 / 544 anschauen.