Ein Prisma hat ja:
* Oben und unten die Grundfläche, die ein beliebiges Vieleck sein kann, und
* Rundherum den Mantel, der aus Rechtecken besteht.
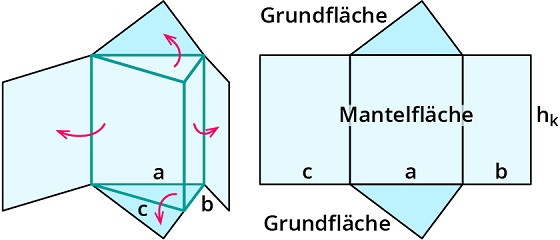
Für die Oberfläche gehst du am Besten so vor:
Arbeitsplaner 3b
Di, 12. 5. 2020
Heute schaut euch bitte an, was wir in Physik zum Thema Elektrizität angefangen hatten.
Lies dir die Hefteinträge und im Buch S. 60 durch. Du solltest wissen:
Wenn es Unklarheiten gibt, kannst du mich gerne auf showbie fragen!
Wenn du am PC / Notebook arbeitest, kannst du dann eine freiwillige Aufgabe lösen:
Mo, 11. 5. 2020
Als Vorbereitung für nächste Woche wiederholen wir heute etwas Chemie.
Ich habe das Wichtigste von Säuren und Basen hier zusammengeschrieben.
Lies es dir durch, dann beantworte diese Fragen:
1. Was sind die Merkmale einer Säure? (Ionen, pH)
2. Was sind die Merkmale einer Base? (Ionen, pH)
3. Ergänze: Starke Säure - Schwache Säure - Starke Base - Schwache Base - Neutral
a) pH = 8: ...
b) pH = 1,5: ...
c) pH = 6,1: ...
d) ph = 13: ...
e) pH = 7: ...
4. Säure oder Base?
a) HCl: ...
b) NaOH: ...
c) NH3: ...
d) H2SO4: ...
Do, 30. 4. 2020
Wer alle Aufgaben seit Freitag, 24.4. gemacht hat, macht noch im ÜB S. 103. Es funktioniert wie gestern, auch hier musst du die fehlende Seite mit dem pythagoräischen Lehrsatz berechnen.
(Achte darauf, ob a, b oder c fehlt!)
Wenn du nicht alles hast, mach ZUERST die fehlenden Aufgaben, sonst kennst du dich bei den heutigen Aufgaben nicht aus!
Mi, 29. 4. 2020
Heute wiederholen wir kurz den pythagoräischen Lehrsatz, weil man ihn für einige Berechnungen braucht.
Zur Erinnerung:
Die Hypotenuse berechne ich so:
Bsp.: a = 5 cm; b = 9 cm; c = ?
Ich fange an mit: a² + b² = 5 x 5 + 7 x 7 = 25 + 81 = 106
Jetzt berechne ich mit dem Taschenrechner am Handy die Wurzel aus 106:
√ 106 = 10,2956...
Ich runde auf mm: c = 10,3 cm
(Ich muss das Handy quer halten, damit der Taschenrechner das Wurzelzeichen √ anzeigt)
Eine Kathete berechne ich so:
Bsp.: a = 5 cm; c = 9 cm; b = ?
Ich fange an mit: c² - a² = 9 x 9 - 5 x 5 = 81 - 25 = 56
Jetzt berechne ich mit dem Taschenrechner am Handy die Wurzel aus 56:
√ 56 = 7,4833...
Ich runde auf mm: b = 7,5 cm
Ü 29.4.1
Berechne die fehlenden Seiten dieser rechtwinkligen Dreiecke:
a) a = 10 cm; b = 6 cm; c = ?
b) a = 3,5 cm; c = 9 cm; b = ?
c) b = 11 cm; c = 17 cm; a = ?
Ü 29.4.2
Berechne nun die Oberfläche von diesem Prisma:
Grundfläche: Rechtwinkliges Dreieck mit a = 4 cm; b = 6,5 cm
Höhe h = 8 cm
Mo, 27. 4. 2020
Wenn du die Aufgaben vom Freitag verstanden hast, mach nun folgende Übungen:
BS 198 / 557 g), h) und i).
ÜB S. 100 a), b) und c).
Fr, 24. 4. 2020
Heute geht es um die Oberfläche von allgemeinen Prismen.
Ein Prisma hat ja:
* Oben und unten die Grundfläche, die ein beliebiges Vieleck sein kann, und
* Rundherum den Mantel, der aus Rechtecken besteht.

Für die Oberfläche gehst du am Besten so vor:
1.) Berechne den Flächeninhalt der Grundfläche (G).
Dazu brauchst du die Flächenformeln, die wir im Februar gelernt haben.
2.) Berechne den Umfang der Grundfläche (u).
3.) Für die Mantelfläche multiplizierst du diesen Umfang mit der Höhe des Prismas:
M = u * h
4.) Jetzt musst du nur noch die Flächen zusammenzählen:
Oberfläche = 2 * Grundfläche + Mantel
O = 2 * G + M
Beispiel: Ein Prisma mit der Höhe h = 6 cm hat als Grundfläche ein Parallelogramm mit a = 8 cm; b = 3 cm; ha = 2 cm.
1.) Wir erinnern uns an die Flächenformel für das Parallelogramm: A = a * ha
Für die Grundfläche rechnen wir also:
G = 8 * 2 = 16 cm²
2.) Für den Umfang zählen wir alle Seitenlängen zusammen:
u = 2 * a + 2 * b
u = 2 x 8 + 2 x 3 = 22 cm
3.) Nun berechnen wir den Mantel:
M = u * h
M = 22 x 6 = 132 cm²
4.) Für die Oberfläche rechnen wir nun:
O = 2 * G + M
O = 2 x 16 + 132 = 32 + 132 = 164 cm²
Aufgabe Ü24.4
Berechne nun die Oberfläche der folgenden Prismen. Wenn du dich genau an die 4 Schritte hältst,
sollte es nicht schwierig sein.
a) Grundfläche: Parallelogramm mit a = 4 cm; b = 4 cm; ha = 3 cm.
Höhe h = 10 cm
b) Grundfläche: Parallelogramm mit a = 7 cm; b = 5 cm; ha = 2,5 cm.
Höhe h = 11 cm
c) Grundfläche: Rechtwinkliges Dreieck mit a = 3 cm; b = 4 cm; c = 5 cm.
Höhe h = 7 cm
(Vergiss nicht, bei der Fläche des Dreiecks durch 2 zu dividieren!)
d) Grundfläche: Rechteck mit a = 5 cm; b = 2 cm
Höhe h = 3 cm
Vergleiche dein Ergebnis mit dem Quader vom Dienstag, 21. 4. (Aufgabe 21.4.2 a)
Mi, 22. 4. 2020
Wenn du die Übungen von gestern richtig gerechnet hast, mache heute:
BS 202 / 570 a) und b)
BS 198 / 557 a) bis f)
Die Oberfläche der anderen Prismen schauen wir uns morgen an. (Wer will, darf es natürlich auch schon heute versuchen!)
Di, 21. 4. 2020
Nun schauen wir uns an, wie man die Oberfläche von Prismen berechnet.
Heute beginnen wir erst mal mit Quadern und Würfeln.
Beim Würfel ist es am Einfachsten. Ein Würfel hat 6 gleich große Quadrate als Flächen, daher rechnet man:
Oberfläche = 6 * Seite * Seite
Ein Würfel mit Kantenlänge 3 cm besteht aus 6 Quadraten mit der Fläche 3 x 3 = 9 cm².
Seine Oberfläche beträgt daher 6 x 3 x 3 = 54 cm².
Aufgabe 21.4.1
Berechne die Oberfläche der folgenden Würfel:
a) a = 2 cm; b) a = 7 m; c) a = 0,2 m
Beim Quader ist es etwas komplizierter. Ein Quader besteht aus 6 Rechtecken, von denen zwei
gegenüberliegende Flächen jeweils gleich groß sind.
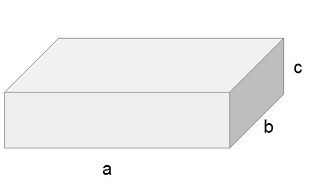
2 Rechtecke (oben und unten) haben die Fläche a * b
2 Rechtecke (vorne und hinten) haben die Fläche a * c
2 Rechtecke (links und rechts) haben die Fläche b * c
Für die Oberfläche muss ich also rechnen:
Oberfläche = 2 * a * b + 2 * a * c + 2 * b * c
oder einfacher:
O = 2 * (ab + ac + bc)
Ein Quader mit den Kantenlängen a = 2 cm; b = 6 cm; c = 1 cm hat also
2 Rechtecke mit 2 x 6 = 12 cm²; 2 Rechtecke mit 2 x 1 = 2 cm² und 2 Rechtecke mit 6 x 1 = 6 cm².
O = 2 x (12 + 2 + 6) = 40 cm².
Aufgabe 21.4.2
Berechne die Oberfläche der folgenden Quader:
a) a = 5 cm; b = 2 cm; c = 3 cm
b) a = 13 mm; b = 4 mm; c= 7 mm
c) a = 0,2 m; b= 30 cm; c = 150 mm (Achtung! Hier musst du erst die Längen in die selbe Einheit umwandeln!)
Mo, 20. 4. 2020
Damit wir das Prozentrechnen nicht verlernen, gibt es zum Aufwärmen ein paar Übungen. Rechne im Kopf:
P 1) Wie viel sind 75 % von 12 €?
P 2) Wie viel sind 50 % von 33 m?
P 3) Wie viel sind 10 % von 382,9?
P 4) Wie viel sind 3 % von 200?
Löse nun BS 201 / 567 und BS 202 / 570 (Nur das Volumen)
Zur Erinnerung: die Fläche eines Dreiecks ist Seite * Höhe / 2
Für einen Pluspunkt kannst du auch noch 573 a) versuchen. Achte auf die unterschiedlichen Einheiten!
Mi, 15. 4. 2020
Guten Morgen!
Ich hoffe, ihr hattet schöne Osterferien.
Für den Anfang wiederholen wir das Volumen des Prismas. Macht die Übungen BS. 200 / 563, 564 und 565, die sollten nicht zu schwer sein.
Hinweis: Die Masse berechnest du, indem du das Volumen mit der Dichte multiplizierst!
Do, 2. 4. 2020
Heute schauen wir uns nur ein paar Beispiele für das Volumen von Quader und Pyramide an.
Lass bei den Übungen die Oberflächen weg; die schauen wir uns später an!
613 - Nur das Volumen der beiden Körper. Die Seitenhöhe ha brauchst du dafür nicht!
615 - Nur a)
622 - Nur b), c) und d)
Mi, 1. 4. 2020
Heute üben wir die Umrechnung von Längen-, Flächen- und Volumseinheiten.
Zur Erinnerung:
1 cm = 10 mm
1 cm² = 100 mm² (= 10 mm x 10 mm)
1 cm³ = 1000 mm³ (= 10 mm x 10 mm x 10 mm)
1 m = 100 cm
1 m² = 10 000 cm²
1 m³ = 1 000 000 cm³
1 m = 1 000 mm
1 m² = 1 000 000 mm²
1 m³ = 1 000 000 000 mm³
Beispiele:
7,5 cm = 75 mm (Das Komma wird um eine Stelle verschoben.)
7,5 cm² = 750 mm² (Das Komma wird um zwei Stellen verschoben.)
7,5 cm³ = 7500 mm³ (Das Komma wird um drei Stellen verschoben.)
75 cm = 0,75 m (Das Komma wird um zwei Stellen verschoben.)
75 cm² = 0,0075 mm² (Das Komma wird um vier Stellen verschoben.)
75 cm³ = 0,000 075 mm³ (Das Komma wird um sechs Stellen verschoben.)
Versuche nun die Aufgaben:
|
a) |
b) |
c) |
|
d) |
e) |
f) |
|
g) |
h) |
i) |
Di, 31. 3. 2020
Heute schauen wir uns
Die Pyramide
an. Eine Pyramide hat eine Grundfläche wie ein Prisma, aber eine Spitze.
Schau dir im Buch den Info-Kasten S. 204 an, dann versuche Übung 581.
(Ohne Begründung. Schreib mir nur die Nummern der Pyramiden.)
Das Volumen einer Pyramide ist genau ein Drittel von einem Prisma.
Also:
Volumen = Grundfläche * Höhe : 3
Versuche jetzt noch BS 210 / 603 und 605
Bei 605: Volumen für alle!
Masse ist freiwillig!
(Für die Masse berechne erst mal das Volumen, dann multipliziere das Volumen mit der Dichte.
Beispiel: Eine Pyramide hat ein Volumen von 70 cm². Dann wäre die Lösung:
Glaspyramide: m = 70 * 2,5 = 175 g
Korkpyramide: m = 70 * 0,24 = 16,8 g
Aluminiumpyramide: m = 70 * 2,7 = 189 g)
Mo, 30. 3. 2020
Hier findest du die Lösungen zu den Gleichungen:
Lösungsblatt zu den Gleichungen
Ich habe zu jeder Gleichung einen möglichen Lösungsweg genau beschrieben. Es gibt noch andere Möglichkeiten, daher
schauen deine Rechnungen vielleicht etwas anders aus. Wichtig ist aber, dass du die selbe Lösung findest!
Diese Woche geht es um geometrische Körper. Schau dir erst mal
diese Übersicht an, dann lies weiter!
Das Prisma (Mehrzahl: die Prismen)
Ein (gerades) Prisma hat:
- Eine Grundfläche ("Boden"): das kann ein Dreieck, Viereck, Fünfeck... sein.
- Eine Deckfläche ("Deckel"), die gleich groß wie die Grundfläche und parallel dazu ist.
- Einen Mantel, der aus Rechtecken besteht.
Beispiele hast du im Buch auf der Seite 195 abgebildet.
Spezialfälle sind:
-Ein Quader besteht nur aus Rechtecken.
-Ein Würfel besteht nur aus Quadraten.
Aufgabe 1 (freiwillig!): Schneide aus dem Buch die Modelle vom Quader (S. 273);
vom dreiseitigem Prisma (S. 281) und vom sechsseitigem Prisma (S. 283) aus und baue sie zusammen.
Aufgabe 2 (für alle): BS 200 / 562. Berechne das Volumen. Die Formel ist:
Volumen = Grundfläche * Höhe
Vergiss nicht auf die richtige Einheit!
Wenn du in cm rechnest, ist das Volumen in cm³.
Wenn du in m rechnest, ist das Volumen in m³.
Wenn du in dm rechnest, ist das Volumen in dm³; da kannst du auch Liter (l) schreiben.
++ Aufgabe 3 Wenn du es gut verstanden hast, kannst du auch BS 201 / 566 versuchen.
Hier musst du erst die Fläche vom Viereck berechnen und dann mit der Körperhöhe multiplizieren.
Du kannst diese Aufgabe aber auch auslassen.
Viel Erfolg!
Fr, 20. 3. 2020
* Herr Schäfer hat mir ein Übungsblatt für Gleichungen geschickt. Ich werde nächste Woche jeden Tag ein paar Übungen davon auf showbie aufgeben.
Falls sich jemand das ganze Blatt schon mal anschauen möchte, stelle ich es hier her:
Übungsblatt zu den Gleichungen
Mi, 18. 3. 2020
* Eine Übung zu den Verhältnissen: Im Übungsbuch S. 63 / 2, 3 und 4
Di, 17. 3. 2020
* Für den Anfang kannst du die Übungen vom Übungsblatt für die Schularbeit, die nicht in der Schule gemacht wurden, fertig stellen. Poste die Lösungen bitte auf my.showbie.com!
Falls du das Übungsblatt nicht hast, findest du hier die Angaben.